北大音像出版社初中数学代数知识点总结
北大音像出版社官网为广大初中生总结的初中代数知识点,可以帮助学生在学习过程中迅速掌握代数学习分要点,考前复习可以巩固初中数学的的知识。
一、数的分类
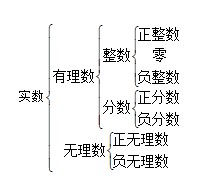
或:
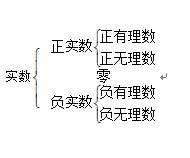
或
其中:有理数(即可比数)即有限小数或无限循环小数;无理数即无限不循环小数。
二、 数轴
(1)三要素:原点、正方向、单位长度。
(2)实数 数轴上的点。
(3)利用数轴可比较数的大小,理解实数及其相反数、绝对值等概念。
三、 绝对值
(1)几何定义:数轴上,表示数a的点与原点的距离叫做数a的绝对值,记做 。
(2)代数定义: = 四、 相反数、倒数
(1)a、b互为相反数 a+b=0(或a=-b);
(2)a、b互为倒数 a·b=1(或a= )。
五、几个非负数
(1) ≥0;
(2)a ≥0;
(3) ≥0(a≥0)。
(4)若几个非负数之和为0,则这几个非负数也分别为0.
六、
(1)a n叫做a的n 次幂,其中,a叫底数,n叫指数。
(2)若x =a(a≥0),则x叫做a的平方根,记做± ;算术平方根记做 。
(3)若x =a,则x叫做a的立方根,记做 。因此 =a
(4)算术平方根性质:
①( ) =a (a≥0);
② = ;
③ (a≥0,b≥0);
④ (a≥0,b>0)。
七、运算顺序:
1. 同 级:左→右
2. 不同级:高→低(先乘方和开方,再乘除,最后加减)
3. 有括号:里→外(先去小括号、再去中括号、最后去大括号)
八、a>0
①(-a) 2n +1 = - a 2n +1
②(-a) 2n = a 2n
九、有理式
(1)有理式 (2)乘法公式
平 方 差:(a+b)(a—b)= a 2 - b 2
完全平方: (a±b)2 =a 2±2a b+ b 2
(3)分式的基本性质:
= (用于通分)= (用于约分)(m≠0)
十、整数指数幂
(1) 零指数幂a0=1(a≠0);负指数幂a -n= (a≠0,n为正整数);
(2) 幂的乘方:①a m a n=a m +n(a>0,m、n为整数);
② (a m) n =a m n(a>0,m、n为整数);
③ (ab) n =a nb n(a>0,b>0,n为整数)。
第二章 方程与不等式
一、一元一次方程
(1)一元一次方程:变形后可化为a x =b(a≠0)的形式,它的解为x = 。
(2)解一次方程的一般步骤:①去分母;②去括号;③移项;④合并同类项;⑤系数化为1。
二、一元二次方程
(1)一元二次方程:变形后可化为a x 2 + b x +c =0(a≠0)的形式,
它的根为x = (b 2 -4ac ≥0 ),(即求根公式)。
(2)解二次方程的常用解法:①求根公式法;②因式分解法;③配方法。
(3)根的判别式:⊿=b 2 -4ac
当b 2 -4ac >0时,方程有两个不等实数根;
当b 2 -4ac =0时,方程有两个相等实数根;
当b 2 -4ac <0时,方程没有实数根。
(4)韦达定理:形如x 2 + p x +q =0,当p 2 -4q ≥0时,设这个方程的两实数根为x1、x2,则有x1+ x2=-p,x1x2=q 。
三、分式方程
(1)分式方程:分母中含未知数的有理方程。
(2)解分式方程的实质:去分母(两边乘方程中各分式的最简公分母),转化为整式方程来解。
(3)注意:有时会产生增根,必须验根。
四、二元一次方程组
(1)基本思路:通过“消元”, 转化为一元一次方程来解。
(2)常用解法:①代入消元法;②加减消元法。
(3)以二元一次方程组的解为坐标的点组成的图象是一条直线。
五、(1)不等式:用不等号(>,<,≥,≤,≠)表示不等关系的式子。
(2)不等式基本性质:
①如果a >b,那么a + c >b + c,a — c >b— c ;
②如果a >b,并且c >0,那么a c >b c, > ;
③如果a >b,并且c<0,那么a c <b c, < 。
(3)解一元一次不等式的一般步骤:①去分母;②去括号;③移项;④合并同类项;⑤系数化为1(此步骤要注意不等号可能变方向)。
六、一元一次不等式组的解集:(设a<b)
①不等式组 的解集是x >b;
②不等式组 的解集是x <a;
③不等式组 的解集是a < x <b;
④不等式组 无解。
第三章 函数
一、函数
(1)定义:设在某变化过程中有两个变量x、y,对于x的每一个值,y都有唯一的值与之对应,那么就说x是自变量,y是因变量,此时,也称y是x的函数。
(2)本质:一一对应关系或多一对应关系。
有序实数对 平面直角坐标系上的点
(3)表示方法:解析法、列表法、图象法。
(4)自变量取值范围:
对于实际问题,自变量取值必须使实际问题有意义;
对于纯数学问题,自变量取值必须保证函数关系式有意义:
①分式中,分母≠0;
②二次根式中,被开方数≥0;
③整式中,自变量取全体实数;
④混合运算式中,自变量取各解集的公共部份。
二、正比例函数与反比例函数
两函数的异同点
#FormatTableID_5#
二、一次函数(图象为直线)
(1)定义式:y=kx+b (k、b为常数,k≠0);自变量取全体实数。
#FormatTableID_6#
(2)性质:
①k>0,过第一、三象限,y随x的增大而增大;
k<0,过第二、四象限,y随x的增大而减小。
②b=0,图象过(0,0);
b>0,图象与y轴的交点(0,b)在x轴上方;
b<0,图象与y轴的交点(0,b)在x轴下方。
三、二次函数(图象为抛物线)
(1)自变量取全体实数
一般式:y=ax2+bx+c (a、b、c为常数,a≠0),其中(0,c)为抛物线与y轴的交点;
顶点式:y=a(x—h)2+k (a、h、k为常数,a≠0),其中(h,k)为抛物线顶点;
h=- ,k= 零点式:y=a(x—x1)(x—x2)(a、x1、x2为常数,a≠0) 其中(x1,0)、(x2,0)为抛物线与x轴的交点。x1、x2 = (b 2 -4ac ≥0 )
(2)性质:
①对称轴:x=- 或x=h;
②顶点:(- , )或(h,k);
③最值:当x=- 时,y有最大(小)值,为 或当x=h时,y有最大(小)值,为k ;
④
#FormatTableID_7#
第四章 统计
一、基本概念
(1)普查与抽样调查、总体与个体
(2)样本与样本容量(无单位)
注明:当样本在总体中合适或具有典型性时,才可从局部结论推广到整体;
不同抽样数据有差异。
(3)频数与频率
频率= 注:频数之和=总次数;频率之和=1。
二、基本计算公式
(1)刻画一组数据的集中程度
①平均数;
算术平均数: = (x 1+x 2+…+x n)
加权平均数: = ,(其中wi为权重,w1+w2+…+wk可以为1)
= ,(其中fi为频数,f1+f2+…+fk = n)
②中位数;
③众数(可以不是数字)。
(2)刻画一组数据的离散或波动程度
①极差;
极差=最大值—最小值
②方差;
S 2= [(x 1— )2+(x 2— )2+…+(x n— )2)]
③标准差。
S = (标准差比方差常用)
三、统计图表
(1)统计表格(其中频数分布表格较常用)
(2)统计图形
①条形统计图;②折线统计图;③扇形统计图;④频数分布直方图:⑤频数折线图 …
第五章 概率
一、必然事件、不可能事件、不确定事件
P(必然事件)=1; P(不可能事件)=0; 0<P(不确定事件)<1。
二、求概率
(1)用模拟实验的方法估计算概率
(2)用树状图和列表法计算概率
注意:等可能性与游戏规则的公平性;不放回与有放回情形。
关键词: 北大音像 | 新ces学习法 返回列表小学英语学习怎样入门: 小学英语学习怎样快速入门呢?小学英……
《北大音像出版社新CES学习法》数理化《 北大音像出版社新CE……
北大音像出版社新CES学习法价钱是多少?北大音像出版社新CES学习……